Geometry (e.g., curves, surfaces, solids) is pervasive throughout the airplane industry. At The Boeing Company, the prevalent way to model geometry is the parametric representation. For example, a parametric surface, S, is the image of a function
S:D → ℝ³
where D ≔ [0..1]×[0..1] is the parameter domain.
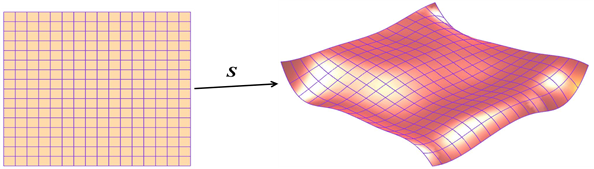
Here S denotes the parametrization, as well as the (red) surface itself.
A geometry’s parametric representation is not unique and the accuracy of analysis tools is often sensitive to its quality. In many cases, the best parametrization is one that preserves lengths, areas, and angles well, i.e., a parametrization that is nearly isometric. Nearly isometric parametrizations are used, for example, when designing non-flat parts that will be constructed or machined flat.
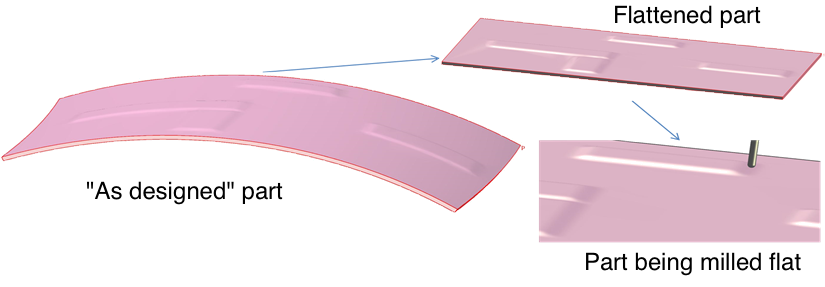
Figure 1. Parts that are nearly developable on one side are often machined on a flat table; then re-formed.
Another area where geometry parametrization is especially important is shape optimization activities that involve isogeometric analysis. In these cases, getting a “good enough” parametrization very efficiently is crucial, since the geometry varies from one iteration to another.
In this project, the students will research, discuss, and propose potential measures of “isometricness” and algorithms for obtaining them. Example problems will be available on which to test their ideas.
References
1. Michael S. Floater, Kai Hormann, Surface parametrization: a tutorial and survey, Advances in Multiresolution for Geometric Modeling, (2005) pp 157—186.
2. J. Gravesen, A. Evgrafov, Dang-Manh Nguyen, P.N. Nielsen, Planar parametrization in isogeometric analysis, Lecture Notes in Computer Science, Volume 8177 (2014) pp 189—212.
3. T-C Lim, S. Ramakrishna, Modeling of composite sheet forming: a review, Composites: Part A, Volume 33 (2002) pp 515—537.
4. Yaron Lipman, Ingrid Daubechies, Conformal Wasserstein distances: comparing surfaces in polynomial time, Advances in Mathematics, vol. 227 (2010) pp. 1047—1077.